4.- TEOREMA DE PITAGORAS

 

Teorema de Pitágoras

Es una fórmula, proveniente de la Geometría Euclidiana denominada así en honor al matemático griego Pitágoras, que establece una relación entre los 3 lados de un triángulo rectángulo. Es decir, conocidos dos de ellos es posible calcular el otro con esta ecuación.

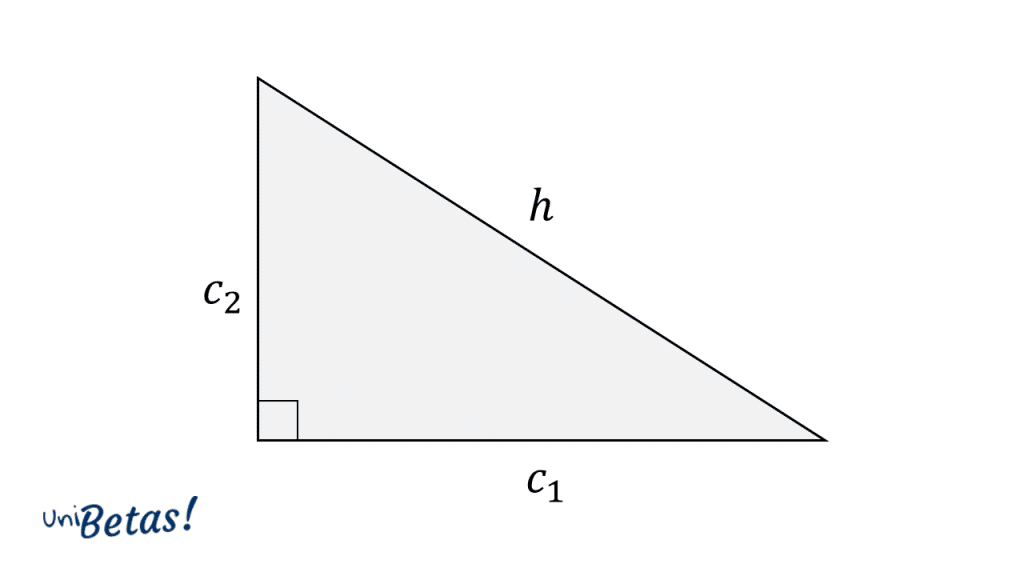
La definición formal del Teorema de Pitágoras establece que:

El cuadrado de la hipotenusa h de un triángulo rectángulo cualquiera, es igual a la suma del primer cateto 1 al cuadrado más el segundo cateto 2 también al cuadrado.

Escrito en lenguaje algebraico, esta relación quedaría como:

${h}^{2}={{c}^{2}}_{1}+{{c}^{2}}_{2}$

Donde ${C}_{1}$ y ${C}_{2}$ son los catetos del triángulo rectángulo. Otra forma de interpretar al Teorema de Pitágoras, es a través de las áreas que forman los cuadrados representados por cada uno de los lados del triángulo rectángulo.

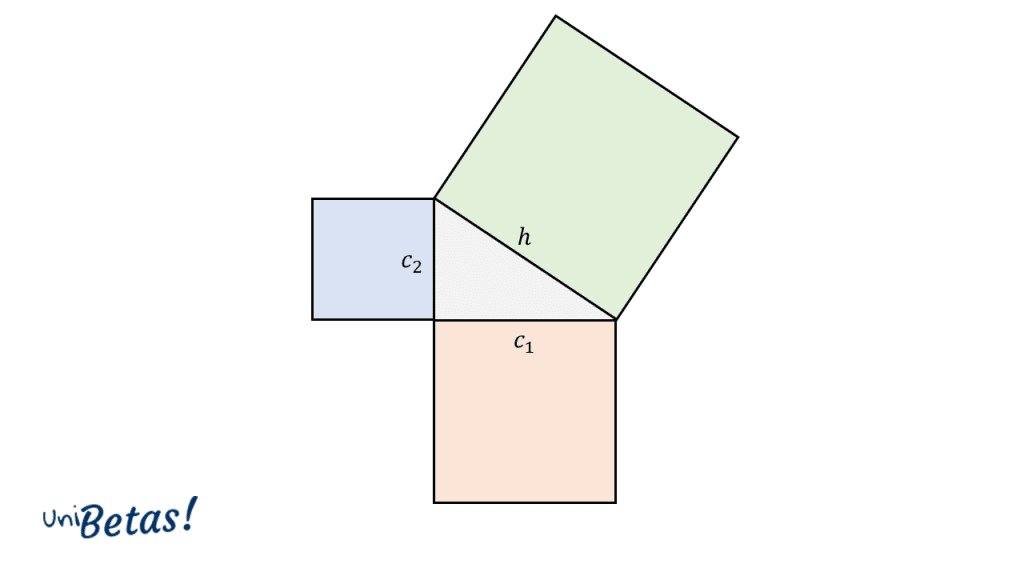
Si a cada uno de los lados del triángulo rectángulo lo asociamos con el lado de un cuadrado, la ecuación del Teorema de Pitágoras nos diría que: el área del cuadrado de lado $h$ es igual a la suma de las áreas de los cuadrados de lado ${C}_{1}$ y ${C}_{2}$.

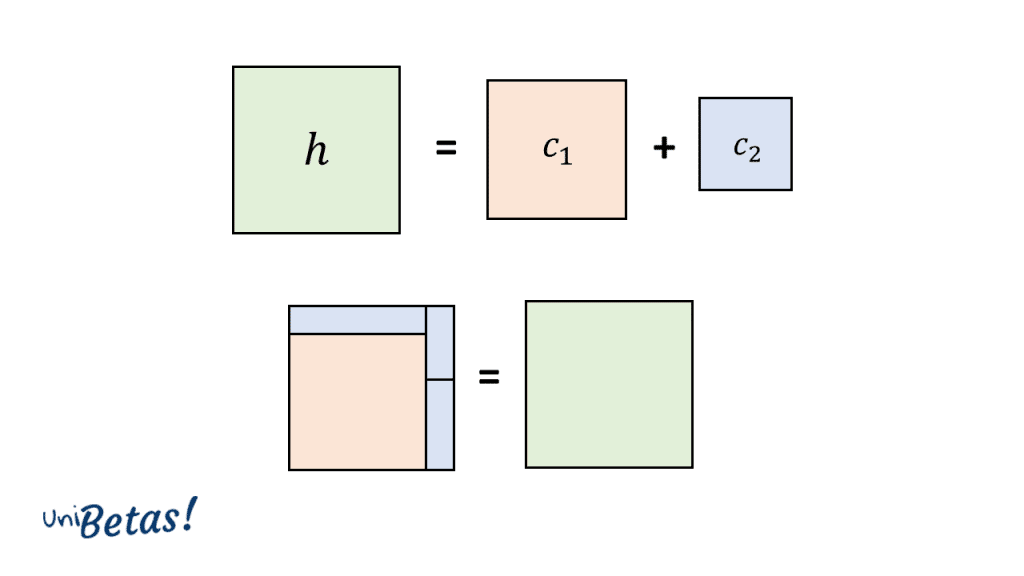
Demostración del teorema de Pitágoras

Existen numerosas vías para demostrar al teorema de Pitágoras, algunas mas gráficas otras recurren al álgebra, en este caso desarrollaremos una alternativa intermedia que puede realizarse con fórmulas y de manera gráfica. Cada paso lo ilustraremos con imágenes para facilitar la demostración.

Supongamos que tenemos un triángulo rectángulo cualquiera con lados $hxy$, donde $h$ es la hipotenusa y tanto $x$ como $y$ son catetos.

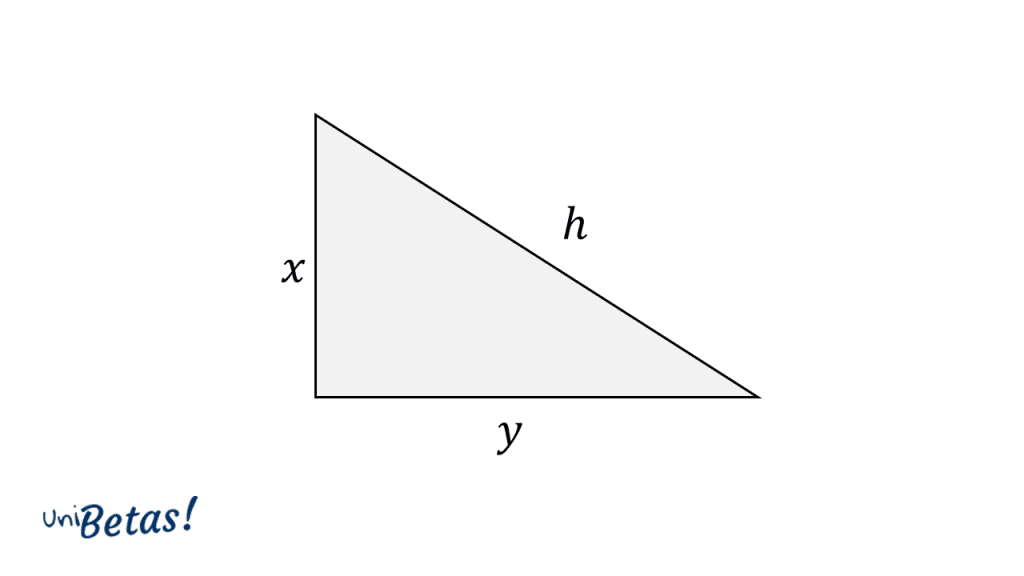
Comencemos por trazar los lados que faltan para formar un cuadrado de lado $h$ que encierre al triangulo rectángulo.

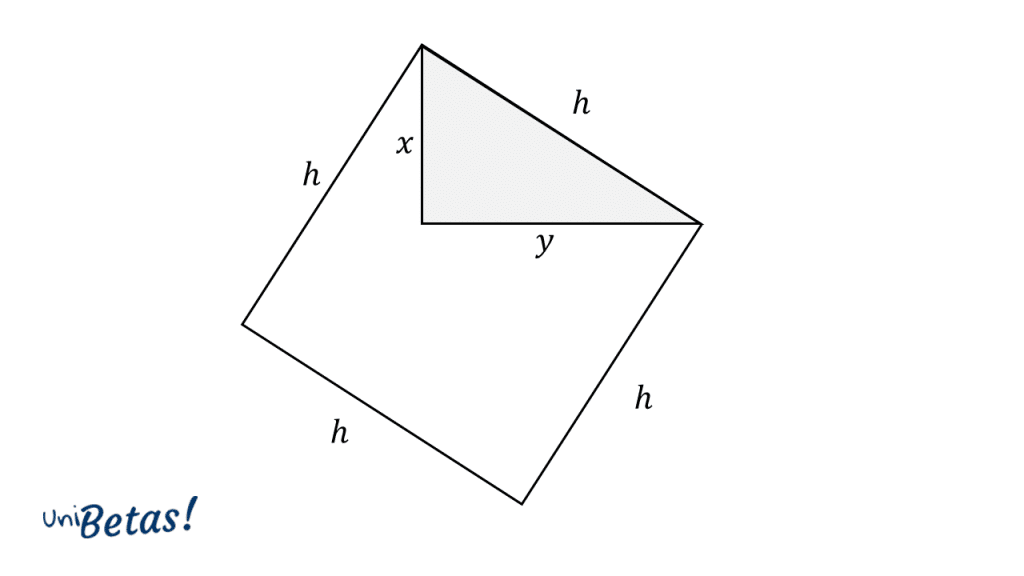
Ahora, vamos a encerrar al cuadrado con otro cuadrado, de tal forma que los vértices del cuadrado de lado $h$ toquen a los lados del nuevo cuadrado. Examinando la figura, vemos como se repite el triángulo inicial $hxy$ en la periferia, apareciendo también las distancias $x$ y $y$ en los lados del nuevo cuadrado.

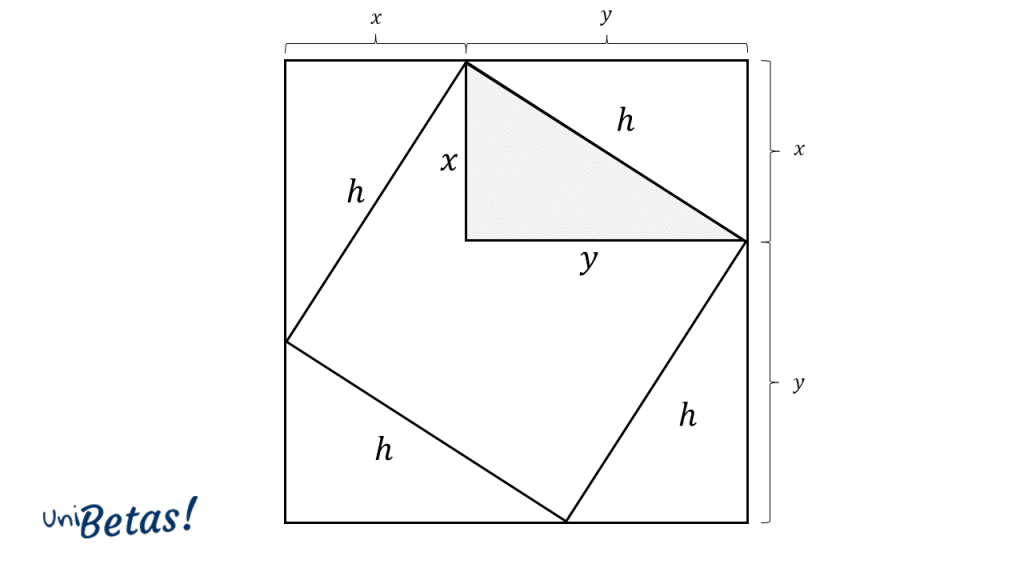
Podemos escribir el área del cuadrado de lado $x+y$ como la suma del área de los triángulos $hxy$ de la periferia mas el área del cuadrado interior de lado $h$.

${\left(x+y\right)}^{2}=4 \frac{x\bullet y}{2}+{h}^{2}$

Desarrollamos.

${x}^{2}+2xy+{y}^{2}=2xy+{h}^{2}$

Simplificamos el término $2xy$ de ambos lados.

${x}^{2}+{y}^{2}={h}^{2}$

Obtenemos finalmente la fórmula del teorema de Pitágoras.

Otra forma de demostrar al teorema de Pitágoras, muy similar a la que hemos recurrido en este caso, hace uso de las áreas de los cuadrados y triángulos que se forman, pero desplazándolas de otra manera.

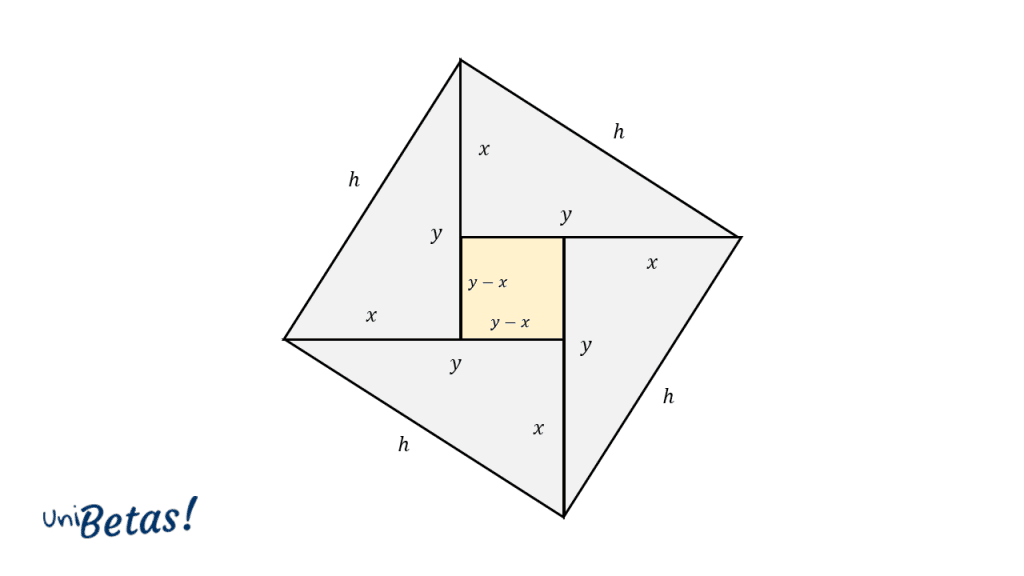
En este caso, vamos como se forma nuevamente el cuadrado de lado $h$ y, dentro de él coexisten 4 triángulos $xyh$ y un cuadrado en el centro de lado $y-x$. Por tanto, podemos escribir el área del cuadrado de lado $h$ como:

${h}^{2}=4\frac{x\bullet x}{2}+{\left(y-x\right)}^{2}$

Desarrollamos y simplificamos la expresión.

${h}^{2}=2xy+{y}^{2}-2xy+{x}^{2}={y}^{2}+{x}^{2}$

Obtenemos, nuevamente, al teorema de Pitágoras.

${h}^{2}={y}^{2}+{x}^{2}$

Teorema de Pitágoras fórmula

La fórmula del teorema de Pitágoras permite determinar un lado desconocido teniendo como dato a los otros dos. A continuación, te presento las variantes del teorema de Pitágoras, con las que podrás determinas cualquiera de los lados de un triángulo rectángulo:

Calcular el lado ${C}_{1}$

${c}_{1}=\sqrt{{h}^{2}-{{c}^{2}}_{2}}$

Calcular el lado ${C}_{2}$

${c}_{2}=\sqrt{{h}^{2}-{{c}^{2}}_{1}}$

Calcular a la hipotenusa

$h=\sqrt{{{c}^{2}}_{1}+{{c}^{2}}_{2}}$

A continuación, te dejo tres ejemplos de aplicación del teorema de Pitágoras con las tres fórmulas anteriores. Ten en cuenta que la ecuación que permite calcular a ${c}_{1}$ o a ${c}_{2}$ es la misma, solo debes considerar que a la izquierda va el lado desconocido y dentro del radical el lado conocido junto a la hipotenusa.

Este conjunto de fórmulas de Pitágoras se conoce como los 3 corolarios del teorema de Pitágoras.

Entre matemáticos expertos en historia de las matemáticas, se dice que es el teorema con más demostraciones en las matemáticas.

El par de demostraciones que hemos adjuntado en este post son apenas una mínima fracción de las existentes incluso.

Ejemplo 1: cálculo de la hipotenusa de un triángulo rectángulo

Dado el triangulo rectángulo de la figura, calcule la longitud de su hipotenusa aplicando el teorema de Pitágoras.

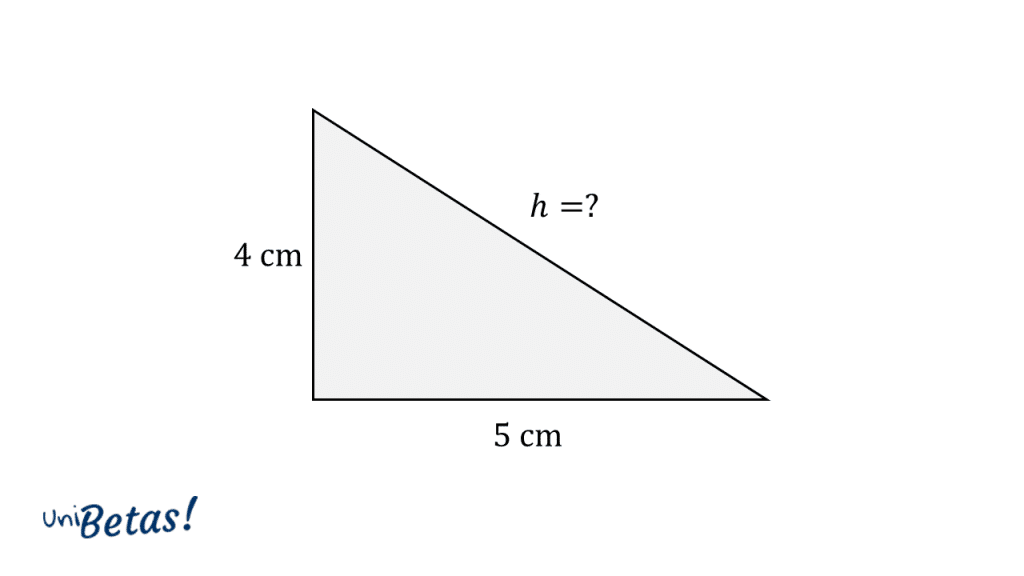
Solución:

Comenzamos por identificar los lados del triángulo. El primer cateto será ${c}_{1}=4$, el segundo ${c}_{2}=5$ y la hipotenusa $h$, la cual es desconocida. Sustituimos los valores en la fórmula para sacar la hipotenusa:

${h}^{2}={c}_{1}^{2}+{c}_{2}^{2}$

Sustituyendo.

${h}^{2}={4}^{2}+{5}^{2}$

Calculamos los cuadrados de 4 y 5.

${h}^{2}=16+25=41$

Ahora, aplicamos raíz cuadrada en ambos miembros para despejar la hipotenusa.

$h=\sqrt{41}$

Podemos concluir este ejemplo aportando dos observaciones. Primero, que no importa el orden que se le dé a los catetos en la ecuación, el resultado será el mismo. Si en lugar de ${c}_{1}=4$ y  ${c}_{2}=5$ hubiésemos escrito ${c}_{1}=5$ y ${c}_{2}=4$, se obtiene que:

$h=\sqrt{{5}^{2}+{4}^{2}}=\sqrt{41}$

Por otro lado, si aprendiste bien sobre el despeje de radicales con índice 2, sabrás que hay dos soluciones: una positiva y otra negativa ¿por qué no escogimos la negativa en lugar de la positiva? Porque en este caso estamos tratando con distancias y estas siempre son positivas.

Ejemplo 2: calcular catetos conociendo la hipotenusa

Determine la longitud del cateto desconocido aplicando la fórmula correcta del teorema de Pitágoras.

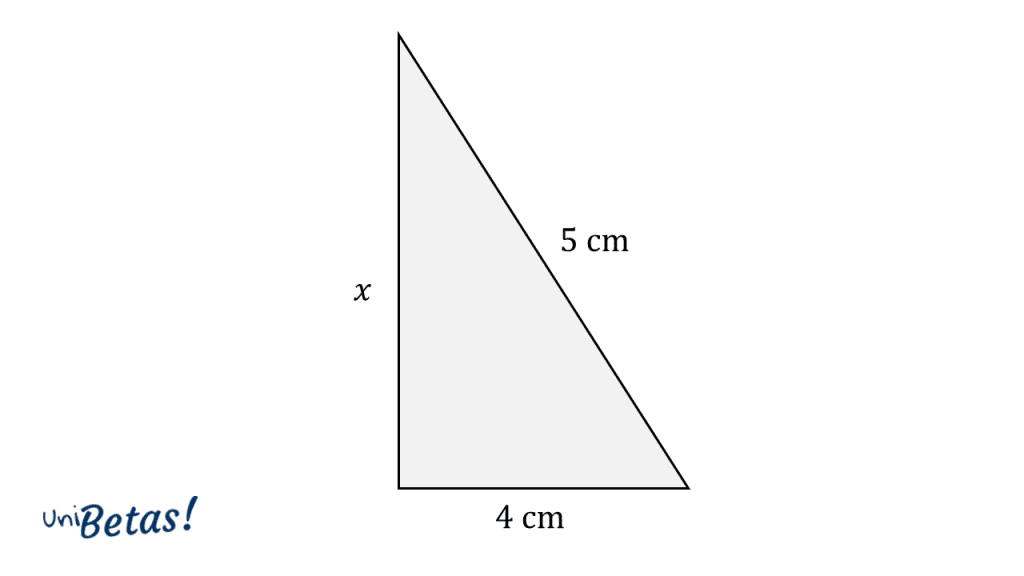
Solución:

Teniendo en cuenta la conclusión dada en el ejemplo anterior, sabemos que podemos calcular la longitud del cateto desconocido aplicando la siguiente ecuación:

$x=\sqrt{{5}^{2}-{4}^{2}}=\sqrt{25-16}$

$x=\sqrt{9}=3$

El cateto restante tiene una longitud de 3 centímetros.

Consideraciones del Teorema de Pitágoras

Recapitulando todo lo mencionado hasta el momento, es necesario aclarar algunas dudas que pueden surgir al utilizar la ecuación de Pitágoras.

• No puede utilizarse para triángulos que no sean rectángulos. Pero si es posible trazar segmentos dentro de un triángulo irregular para formar en su interior triángulos rectángulos

• Como sabes, al despejar una raíz cuadrada el resultado puede ser positivo o negativo. Siempre se toma el resultado positivo porque los lados y las longitudes son siempre positivas
• Los catetos ${C}_{1}$ y ${C}_{2}$ no tienen una distinción particular en la ecuación. Cualquier lado que no sea la hipotenusa puede llamarse ${C}_{1}$ e inmediatamente el otro será el cateto ${C}_{2}$
• En problemas de decidir el camino más corto donde entran en juego triángulos rectángulos, la distancia de la hipotenusa es menor la suma de las longitudes de los catetos $h<{c}_{1}+{c}_{2}$, por tanto, el camino más corto es la hipotenusa

Aplicaciones del Teorema de Pitágoras

Siempre que en un problema se presente un triángulo rectángulo o la necesidad de medir la distancia euclídea más corta entre dos puntos, el Teorema de Pitágoras estará allí para ayudarnos. Algunas de las aplicaciones más comunes son:

• Calcular alguno de los lados de un triángulo rectángulo.
• Determinar si un triángulo es o no rectángulo. Para ello debe cumplirse que:

${h}^{2}={{c}^{2}}_{1}+{{c}^{2}}_{2}$

• Para calcular el módulo de un vector en dos y tres dimensiones.

$‖V‖=\sqrt{{{v}^{2}}_{x}+{{v}^{2}}_{y}}  con V\in {R}^{2}$

$‖V‖=\sqrt{{{v}^{2}}_{x}+{{v}^{2}}_{y}+{{v}^{2}}_{z}}  con V\in {R}^{3}$

• Para medir la distancia entre dos puntos en el plano o el espacio tridimensional.

$d\left(x,y\right)=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}$

$d\left(x,y,z\right)=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}+{\left({z}_{2}-{z}_{1}\right)}^{2}}$

• Los triángulos rectángulos son la base para la descripción de las identidades trigonométricas en la circunferencia unitaria. Se llama unitaria porque tiene radio igual a 1.

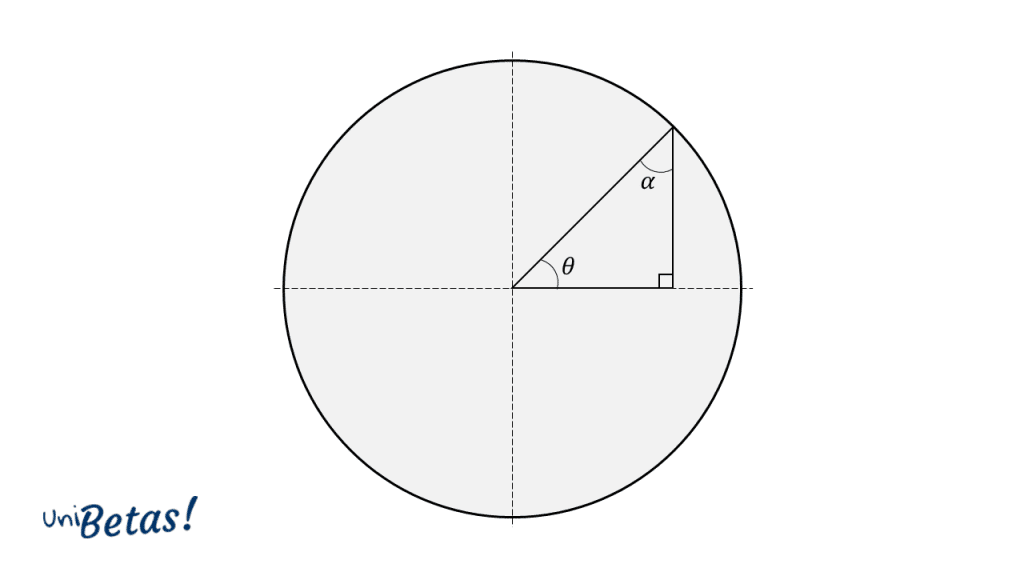
Si tomamos en cuenta el ángulo $\theta$, nos queda la siguiente descomposición en base al teorema de Pitágoras:

$1={\mathrm{sin}}^{2}\theta +{\mathrm{cos}}^{2}\theta$

Esta identidad recibe el nombre de identidad Pitagórica.

• En el modelado matemático de problemas físicos y de análisis matemático. Algunas de estas aplicaciones son:

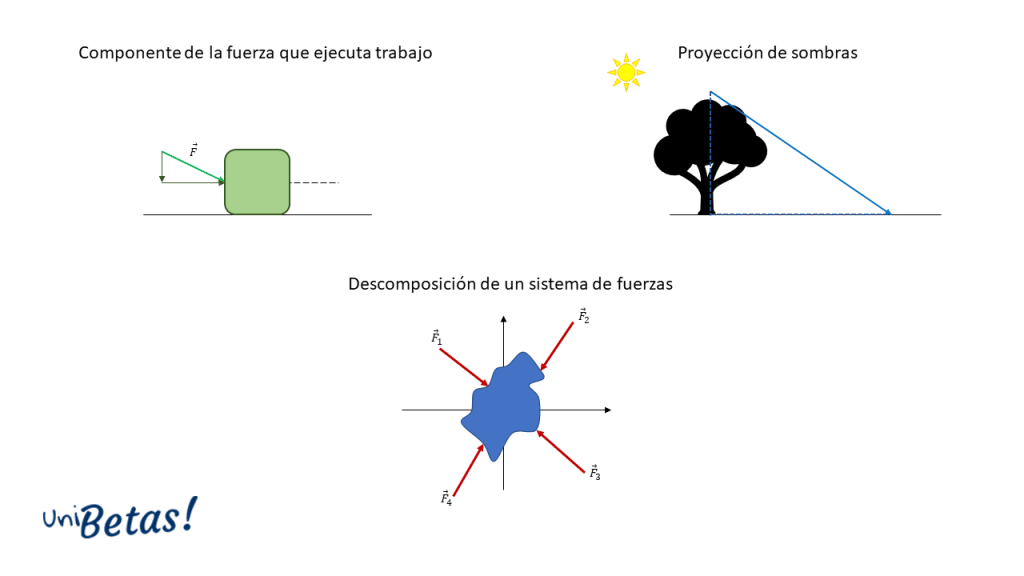
• La altura de una escalera, la sombra de un árbol o un edificio. En general, para problemas en los que es necesario calcular proyecciones.
• Para medir las proyecciones de una fuerza sobre el eje que produce trabajo (teorema del trabajo y la energía). Esto aplica para descomponer cualquier magnitud física de tipo vectorial.
• Al descomponer alguna de las leyes de Newton del movimiento en las componentes de los ejes coordenados.

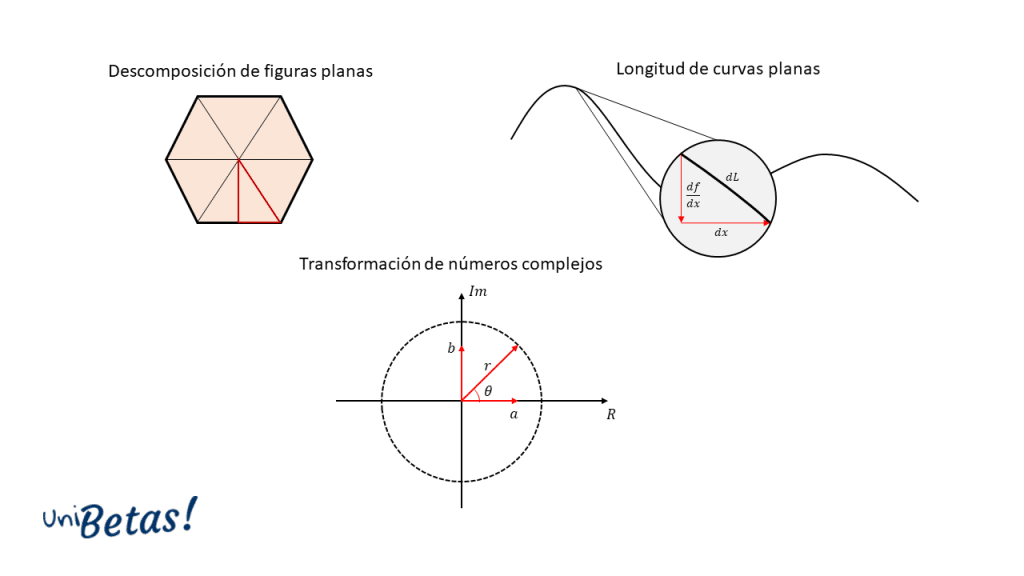
• En geometría plana, para subdividir polígonos regulares como rombos o pentágonos, al momento de analizar propiedades como área, apotema y perímetro.
• En problemas de optimización, la mayoría de las soluciones converge en encontrar triángulos rectángulos para modelar el problema planteado.
• En cálculo integral, el teorema de Pitágoras es fundamental para el método de integración por sustitución trigonométrica, se emplea para medir la longitud de curvas aplicando una descomposición diferencial de la misma en forma de triangulo rectángulo.
• En geometría analítica, el teorema de Pitágoras es fundamental para descomponer vectores y para describir a las secciones cónicas como la circunferencia, parábola, elipse y la hipérbola.
• En números complejos, para transformar de la forma binomial $a+ib$ a la forma exponencial $r{e}^{i\theta }$, el módulo del fasor $r$ se calcula aplicando la fórmula del teorema de Pitágoras.

 

Y estas siguen siendo solo un subconjunto muy pequeño de todas las aplicaciones que posee el teorema de Pitágoras, podríamos entender el montón de demostraciones, como una forma natural del teorema para manifestarse en todas las ramas de las ciencias; no solo en matemáticas y en física.

¿Para qué sirve el Teorema de Pitágoras?

A partir de las secciones anteriores, sabemos que el teorema de Pitágoras permite hallar la longitud de cualquiera de los tres lados de un triángulo rectángulo cuando conocemos dos de ellos, pero en la vida real ¿dónde entra en juego la fórmula de Pitágoras?

Ya que relaciona distancias entre sí, es una fórmula útil a la hora de construir casi cualquier cosa. Los arquitectos e ingenieros de la antigüedad emplearon el Teorema de Pitágoras (muchas veces sin saber que lo que era) para construir puentes, muros y escaleras perfectamente alineados y perpendiculares.

En carpintería, fabricación de piezas mecánicas y estructuras, es una herramienta fundamental para unir por sus extremos piezas para que queden perfectamente perpendiculares entre ellas.

Para la creación de videojuegos 2D y 3D, el Teorema de Pitágoras y la geometría (analítica y elemental) permiten medir distancias entre sólidos para el cálculo de colisiones, velocidades, aceleraciones y trayectorias. Sin ir más lejos, todos los motores gráficos de cualquier aplicación informática implementan el teorema de Pitágoras para la localización de los elementos en ella.

Los sistemas de posicionamiento global, conducción autónoma y CNC (Control Numérico Computarizado), utilizan polígonos y técnicas de triangulación basadas en el teorema de Pitágoras para delimitar zonas, establecer rutas y medir distancias.